È stato pubblicato il nuovo esercizio della rubrica: Gita Turistica.
Ci tengo a precisare che la cadenza con la quale vengono pubblicati tali esercizi è prettamente casuale, nel senso che non è più una rubrica periodica come lo era inizialmente, ma quando pensiamo degli esercizi interessanti da proporre ed abbiamo il tempo di prepararli lo facciamo volentieri 
.
arriverà una soluzione ufficiale come negli altri tai?
La rubrica voleva che l’editorial di ogni esercizio arrivasse alla pubblicazione dell’esercizio successivo, tuttavia è anche vero la frequenza di pubblicazione è ormai ridotta a 0 
. Inoltre manca anche l’editorial dell’ultimo esercizio…
In ogni caso direi che per il momento posso permettermi di darti un piccolo hint: scomponi il problema in 2 parti:
Prova a risolvere i 2 sottoproblemi singolarmente, con quale complessità temporale riesci a farlo?
Riassumendo il testo: esistono N paesi numerati da 0 a N-1 collegati da N-1 strade bidirezionali in modo che ogni coppia di paesi risulta connessa. Ogni paese i ha un proprio cibo tipico con dolcezza pari a d_i, tutte le dolcezze sono diverse tra loro: d_i \neq d_j \forall i,j \mid i \neq j. Verrà selezionato un percorso che parte dal paese 0 e continua ricorsivamente in paese adiacenti a quello attuale che non sono ancora stati visitati. Il percorso termina quando tutti i paese adiacenti a quello attuale sono stati visitati. Man mano che i paesi vengono visitati viene mantenuta una lista ordinata V delle dolcezze dei cibi tipici dei paesi visitati. Ogni paese i ha un CAP C_i e, supponendo di terminare la visita nel paese i Fabio e Giacomo mangeranno il cibo che ha una dolcezza pari a V_{C_i}. Inoltre Fabio sceglierà il secondo, il quarto, … paese da visitare cercando di massimizzare la dolcezza del cibo che mangeranno, mentre Giacomo sceglierà il terzo, il quinto, … paese da visitare cercando di minimizzarla.
Risulta facile notare come l’insieme degli N paesi formi in realtà un albero, e che una possibile visita non è altro che un cammino dalla radice (il nodo 0) a una foglia, dove le scelte di Fabio gli permettono di scegliere nodi con profondità dispari, mentre quelle di Giacomo gli permettono di scegliere nodi con profondità pari.
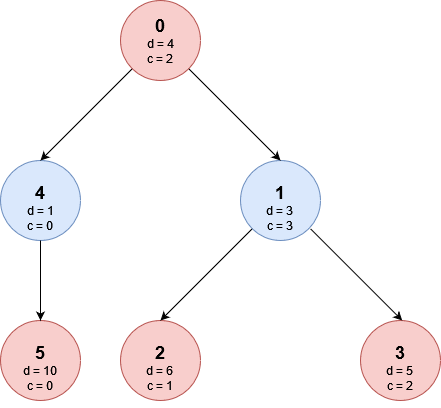
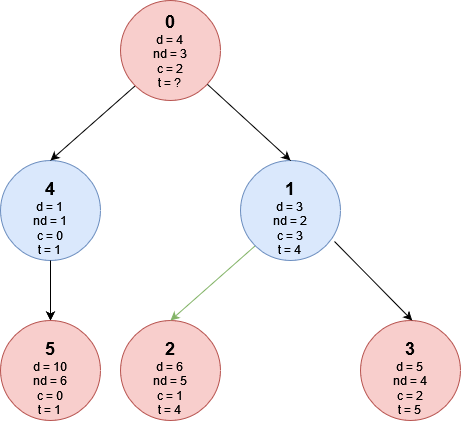
Questo albero rappresenta l’input del caso di esempio:
Dividiamo ora la risoluzione del problema in 2 parti:
Abbiamo notato come esista un numero di percorsi pari al numero di foglie e vogliamo calcolare la dolcezza del cibo tipico che mangeremmo in ognuna di esse, nel nostro caso abbiamo 3 percorsi:
Cerchiamo quindi un modo per computare per ogni foglia x il valore di val(x) ossia la dolcezza del cibo che mangeremmo terminando il percorso nella foglia x. Ci sono molti modi per fare questo passaggio presenterò solo il modo più efficiente.
Vorremmo avere una struttura dati S che ci permette di:
In questo modo potremmo visitare tramite una DFS l’albero descritto precedente e per ogni nodo x fare:
dfs(x):
S.set(d_x) // Attiviamo la dolcezza del valore corrente
for child : children[x]: // Continuo il percorso verso le foglie
dfs(child)
if children[x] is empty(): // Sono arrivato a una foglia
val_x = S.find(c_x) // Trovo la dolcezza scelta per la foglia x
S.unset(d_x) // Disattivo la dolcezza attuale
Inizializzando una struttura S dove inizialmente tutti i valori sono disattivati ed eseguendo la procedura mostrata precedentemente a partire dalla radice (il nodo 0) possiamo individuare per ogni foglia x il valore val(x). Notiamo come la visita abbia una complessità temporale pari al numero di nodi (ricordo che si tratta di un albero): O(N). Dobbiamo vedere ora con complessità riusciamo a eseguire le operazioni set(), unset(), find().
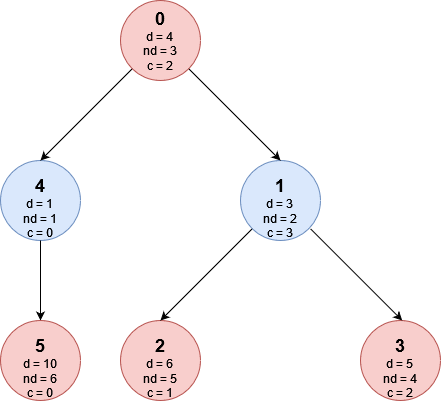
Prima di presentare S svolgiamo un passaggio preliminare che risulta essere necessario per la struttura dati che stiamo cercando, vogliamo restringere il dominio delle varie dolcezze ad [1, N] in modo che vengano rispettare le relazioni di minore e maggiore tra i vari cibi. Tale operazione può essere svolta tramite un ordinamento delle coppie (d_x, x) per poi assegnare le dolcezze in ordine crescente ai piatti seguendo tale ordinamento. Indichiamo con nd_x la nuova dolcezza del nodo x dopo aver ristretto il dominio. Il caso d’esempio diventa dunque:
Possiamo svolgere questo passaggio con una complessità temporale O(NlogN).
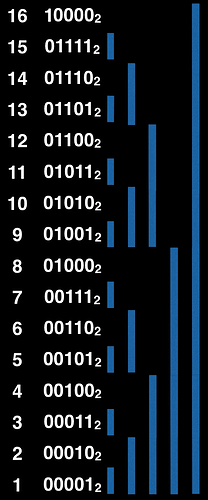
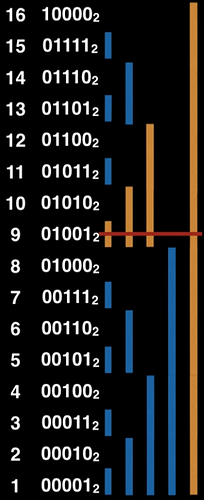
La struttura che utilizzeremo è un fenwick tree, vanta una buona flessibilità e un’ottima efficienza, ma non lo useremo nella sua versione standard, quindi spiegherò anche il suo funzionamento. Per utilizzare questa struttura efficientemente è necessario che i valori siano compresi in [1, N] (ecco il perché del passaggio precedente). Immaginiamo di avere un vettore V indicizzato da 1 a N, il relativo fenwick tree ft che è anche esso un vettore indicizzato da 1 a N rappresenta un albero dove ogni cella risulta “responsabile” di un insieme di celle del vettore V (ossia contiene la somma dei valori in quelle celle), in particolare la posizione dell’LSB (least significan bit) determina l’intervallo di responsabilità che ogni cella ha rispetto al vettore originale, infatti una cella con LSB in posizione x del fenwick tree (contando da destra 0-based), copre 2^x celle del vettore originale. Mostriamo ora l’intervallo di responsabilità di ogni cella di ft rispetto alle celle del vettore originale con 16 elementi
Prima di capire come implementare la funzione find() vediamo come possiamo usare questa struttura per eseguire somme prefisse. In particolare supponiamo di voler computare la somma dei valori nell’intervallo V[1,7] allora possiamo partire dalla cella ft[7] (che contiene la somma degli elementi in V[7, 7], per poi passare dalla cella ft[6] (che contiene la somma degli elementi in V[5, 6]) e infine aggiungiamo la cella ft[4] (che contiene la somma degli elementi in V[1, 4]), in tal modo facendo ft[7] + ft[6] + ft[4] otteniamo la somma degli elementi in V[1, 7]:
Notiamo come per capire quali intervalli coprono un certo intervallo [l, r] partiamo dalla posizione r e sappiamo che quella cella risulta responsabile per se stessa e le 2^{LSB(r)} - 1 celle prima di lei, quindi dopo aver considerato l’intervallo rappresentato da r ci sposteremo in quello rappresentato da r - 2^{LSB(r)}, e così via fino ad arrivare ad r = 0.
Analizziamo la complessità di questa operazione: notiamo come il numero d’iterazioni necessarie corrisponde al numero di bit con valore pari a 1 in r, il caso peggiore si ha quindi quando r = 2^n - 1 ma anche in tal caso bastano O(n) operazioni. Quindi in generale posso ottenere una somma prefissa su un fenwick tree di N elementi in O(logN).
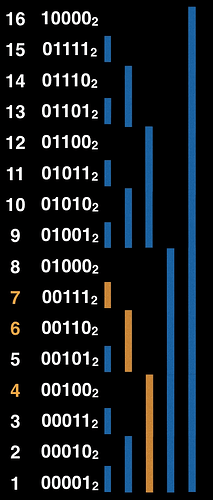
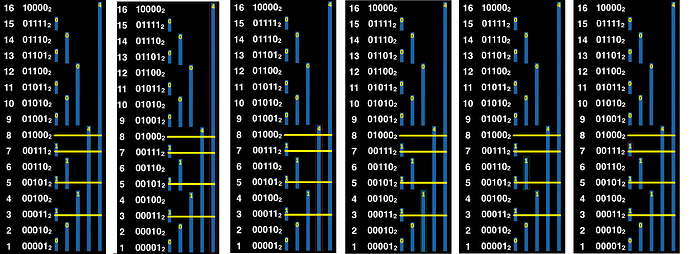
Vediamo quindi come modificare il fenwick tree volendo aggiornare uno degli elementi di V, questo equivale alle operazioni di set() ed unset(). In particolare supponiamo di voler aggiornare il valore V[x] e incrementarlo di k tramite add(x, k), allora con la funzione add() dovremo andare ad aggiornare i valori di tutte le celle di ft il cui intervallo di responsabilità contiene V[x], supponendo che x valga 9:
Per individuare tali celle è sufficiente partire dalla cella x=9 (che sicuramente copre se stessa) e continuare ad aggiungere il valore del suo LSB fino a quando la cella che sto considerando è coperta dall’albero (è minore o uguale a N):
Quindi l’operazione set(i) corrisponde ad add(i, 1) ed unset(i) corrisponde a add(i, -1) (chiameremo set() solo su celle non ancora attivate e unset() solo su celle già attivate).
Vediamo infine come fare l’operazione find(k), per farlo useremo una logica simile alla lower bound. Supponiamo che p sia la posizione che stiamo cercando, inizialmente la inizializziamo a 0 (inizializziamo a 0 anche s ossia la somma prefissa attuale) e procediamo con il settare i bit di p partendo dal più significativo verso quello meno significativo. In particolare quando impostiamo un bit ad 1 dobbiamo verificare che la somma prefissa fino a p rimanga comunque minore di k. Supponiamo di star determinando il valore del bit i, se settando tale bit il valore di p rimane minore di N e il valore di s rimane minore di k allora la posizione che stiamo cercando si trova in (p + 2^i, p + 2^{(i + 1)}] e quindi settiamo il bit i uguale a 1 altrimenti si trova in [p, p + 2 ^ i] e non serve settare il bit i. Infine finiremo nella posizione p tale che \Sigma_{j=1}^{p}V[j] < k ma \Sigma_{j=1}^{p+1}V[j]>=k quindi siamo interessati alla posizione p+1.
Mostriamo un esempio nel quale vengono eseguite le operazioni set(3), set(5), set(7), set(8) e poi viene un eseguita una find(3) ossia siamo interessati a sapere quale è il terzo elemento. Dalla seconda immagine vediamo come non possiamo settare il bit 4 perché s + 4 \geq 3, quindi passiamo al bit 3 e anche in questo caso s + 4 \geq 3 quindi non possiamo settarlo, con i = 2 abbiamo che s + 1 < 3 quindi possiamo settarlo (p diventa 4 e s diventa 1), con i = 1 abbiamo che s + 1 < 3 quindi lo settiamo ad 1 (p diventa 6 e s diventa 2) e infine con i=0 abbiamo che s + 1 \geq 3 quindi non possiamo settare tale bit ad 1. Ricordandoci infine di incrementare p di 1 otteniamo p = 7, proprio l’indice del terzo elemento.
Anche in questo caso il numero di operazioni corrisponde al numero di bit necessari per rappresentare N, abbiamo quindi la struttura che desideravamo che ci permette di fare le operazioni di set(), unset(), find() con complessità pari a O(logN).
Terremo inoltre delle strutture aggiuntive in modo che per ogni nodo i possiamo sapere la sua dolcezza compressa nd_i ed in modo che per ogni dolcezza compressa possiamo risalire alla dolcezza originale del nodo d_i. Eseguiremo quindi l’ordinamento e poi chiameremo la DFS. Nella discesa della DFS aggiorneremo il fenwick settando ad 1 i vari nd_x tramite S.set(nd_i), arrivati ad una foglia chiameremo S.find(C_i) e useremo la struttura ausiliare descritta in precedenza per ottenere in tempo costante la dolcezza del cibo tipico che mangeremmo arrivando in quella foglia ed infine prima di risalire da un nodo eliminiamo la sua dolcezza dalla struttura tramite S.unset(nd_i).
Abbiamo dunque visto come risolvere la parte uno del problema in O(NlogN).
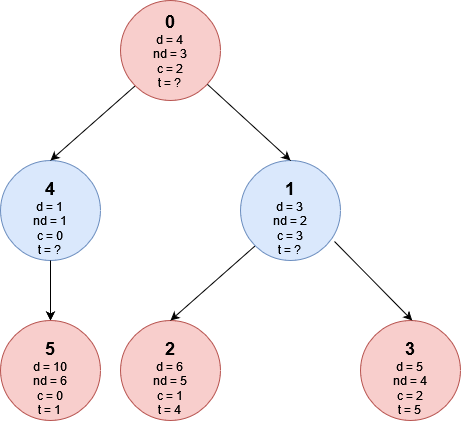
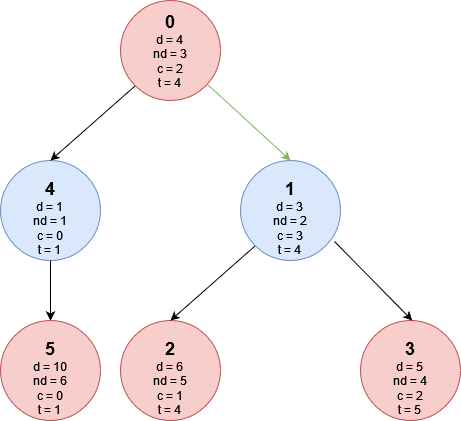
Ora che sappiamo quale cibo mangeremmo terminando il percorso in ognuna delle foglie (ricordo che esiste una relazione biunivoca tra le foglie e le possibili visite della città) vediamo come Fabio e Giacomo effettueranno le loro scelte. Tale algoritmo è conosciuto in letteratura come minmax. Iniziamo però aggiungendo alla rappresentazione dell’albero le dolcezze dei cibi che mangeremmo nelle foglie (identifichiamo questo valore con il simbolo t):
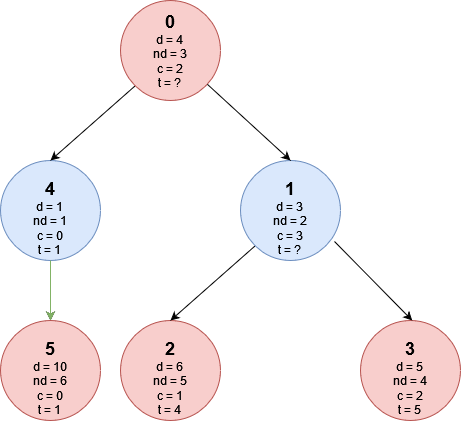
Ora che conosciamo i valori di t nelle foglie possiamo procedere dal basso verso l’alto per capire il valore di t in tutti i nodi, fino a trovare il valore di t_0 che rappresenta la risposta del problema. Partiamo analizzando il nodo 4, essendo il nodo 4 ad una profondità dispari (notare il colore blu) è il turno di Giacomo di scegliere quale paese visitare, ma avendo il nodo 4 un solo figlio Giacomo non ha altra scelta che andare in quello, sapendo che finirà con il mangiare un piatto di dolcezza pari a 1.
Guardiamo ora il nodo 1: la scelta spetta ancora a Giacomo che può decidere di andare verso il nodo 2 finendo con il mangiare un piatto di dolcezza pari a t_2 = 4 oppure andare verso il nodo 3 finendo con il mangiare un piatto di dolcezza pari a t_3 =5. Ricordando che Giacomo ama i cibi salati se si troverà nel nodo 1 sceglierà di andare verso il nodo 2 ottenendo t_1 = t_2 = 4.
Vediamo infine la scelta di Fabio al nodo 0: preferendo cibi dolci Fabio sceglierà di andare verso il nodo 1 sapendo che finirà con il mangiare un piatto con dolcezza maggiore rispetto a quello che mangerebbe andando verso il nodo 4. Quindi t_0 = t_1 = 4, tale valore rappresenta la risposta al nostro problema.
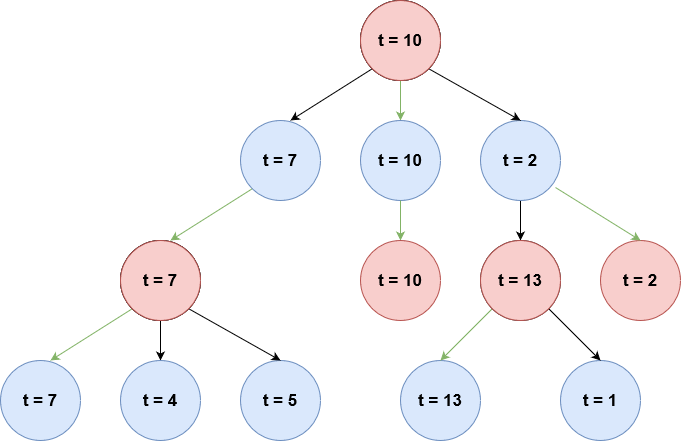
Il nome minmax deriva dal fatto che, riferendomi all’utilizzo attuale, il valore di t nei nodi di profondità dispari corrisponde al minimo valore di t dei figli, viceversa il valore di t nei nodi di profondità pari corrisponde al massimo valore di t dei figli. Qui si può visualizzare tale approccio su un albero più grande:
