Editorial
Yo, dopo una piccola attesa (![]() ) ecco l’editorial del problema.
) ecco l’editorial del problema.
Come al solito procediamo per subtask!
Subtask 1
Il subtask 1 è relativo ai casi d’esempio. Basta restituire l’output desiderato ![]()
int speedrunna(int N, int K, int a, int b){
if(N == 3)return 3;
return 1156;
}
Time complexity: O(1)
Space complexity: O(1)
Subtask 2 & 3
I subtask 2 e 3 sono stati ideati per testare che la soluzione prodotta si calcoli effettivamente i dati dal formato indicato.
L’idea di base era far scopiazzare il codice da cct e adeguarlo all’input.
#include <bits/stdc++.h>
using namespace std;
int speedrunna(int N, int K, int a, int b);
int mul(int a, int b, int mod){
return (a * b) % mod;
}
int fastPow(int b, int e, int mod){
if(e == 0){
return 1;
}
int ans = fastPow(mul(b, b, mod), e / 2, mod);
if(e & 1){
ans = mul(ans, b, mod);
}
return ans;
}
int getTime(int i, int a){
return fastPow(a, i, 1000);
}
int getCharge(int i, int b, int k){
return fastPow(b, i, k);
}
int add(int a, int b){
if(a == INT_MAX || b == INT_MAX)return INT_MAX;
return a + b;
}
int dp(int i, int k, int a, int b, vector<vector<int>> &memo, int K){
if(i == (int) memo[0].size()){
return 0;
}
int &ret = memo[k][i];
if(ret != INT_MAX){
return ret;
}
int time = getTime(i, a);
int charge = getCharge(i, b, K);
if(k == K){
ret = dp(i + 1, 0, a, b, memo, K);
}
ret = min(ret, time + dp(i + 1, min(K, k + charge), a, b, memo, K));
return ret;
}
int speedrunna(int N, int K, int a, int b){
vector<vector<int>> memo(K + 1, vector<int>(N, INT_MAX));
return dp(0, 0, a, b, memo, K);
}
Time complexity: O(N \times K \times log(N))
Si può ridurre la complessità temporale calcolando una volta sola i valori delle cariche e dei tempi richiesti. Lo spazio di memoria a disposizione permette la memorizzazione di questi calcoli.
Space complexity: O(N \times K)
Subtask 4
Il subtask 4 è effettivamente il subtask in cui il problema si differenza dalla sua prima versione.
I limiti di memoria non ci permettono di memorizzare completamente la matrice per tutti gli stati possibili.
Con una soluzione top-down non è intuitivo a colpo d’occhio capire le dipendenze delle nostre transazioni.
Riscrivendo il codice con una soluzione bottom-up è facile notare che i K stati per i-esimo livello dipendono solo dai K del livello i - 1.
Per cui, tenendo i memoria solo i 2K stati interessati riduciamo la complessità spaziale da N \times K a K.
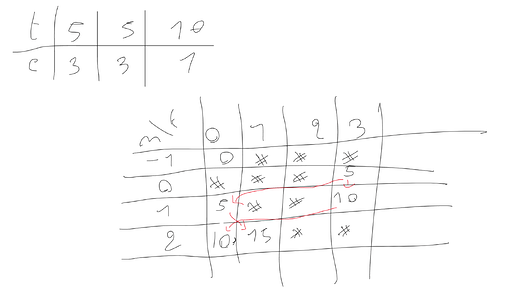
Uno sketch della tabella dei risultati intermedi per il test case di cct 1:
#include <bits/stdc++.h>
using namespace std;
int speedrunna(int N, int K, int a, int b);
int mul(int a, int b, int mod){
return (a * b) % mod;
}
int fastPow(int b, int e, int mod){
if(e == 0){
return 1;
}
int ans = fastPow(mul(b, b, mod), e / 2, mod);
if(e & 1){
ans = mul(ans, b, mod);
}
return ans;
}
int getTime(int i, int a){
return fastPow(a, i, 1000);
}
int getCharge(int i, int b, int k){
return fastPow(b, i, k);
}
int add(int a, int b){
if(a == INT_MAX || b == INT_MAX)return INT_MAX;
return a + b;
}
int speedrunna(int N, int K, int a, int b){
// initiating values first
vector<int> prev(K + 1, INT_MAX), cur(K + 1);
prev[0] = 0;
for(int i = 0; i < N; i++){
fill(cur.begin(), cur.end(), INT_MAX);
int time = getTime(i, a);
int charge = getCharge(i, b, K);
// Just completing the level
for(int k = 0; k <= K; k++){
int index = min(k + charge, K);
cur[index] = min(cur[index], add(prev[k], time));
}
// using the strument
cur[0] = min(cur[0], prev[K]);
swap(prev, cur);
}
return *min_element(prev.begin(), prev.end());
}
Time Complexity: O(N \times K + N log(N) )
Si può ridurre la complessità computando passo per passo le potenze se si processano i livelli dal primo.
Nella soluzione proposta è possibile farlo, rimuovendo cosi il fattore N log (N)
Space Complexity: O(K)
Robe a caso
Il codici proposti nell’editorial sono stati sviluppati da me dopo aver programmato in java per un anno. Sono inutilmente prolissi per questa ragione ![]()