Salve a tutti, sto provando a risolvere il problema yutaka e sto avendo delle difficoltà ad ideare la soluzione con programmazione dinamica (sono alle prime armi). Praticamente quello che ho fatto è stato prima risolvere il problema in maniera brute force (ricorsiva), poi ho osservato l’albero delle chiamate e ho pensato a come si potesse ottimizzare. Alla fine sono arrivato a questo algoritmo solo che non riesco a capire come migliorarlo ulteriormente (se si può fare): (ottengo 49/100)
#include<bits/stdc++.h>
using namespace std;
vector<int> solution(1000001, -1);
int recursive(int pezzi[], vector<int> &posPezzi, int n, int i=1, int spez=-1)
{
if(i==n)
return 1;
if(solution[spez+1]!=-1)
return solution[spez+1];
if(posPezzi[i]>spez)
return solution[spez+1]=recursive(pezzi, posPezzi, n, i+1, i-1)%1000000007;
return solution[spez+1]=(recursive(pezzi, posPezzi, n, i+1, spez)%1000000007+recursive(pezzi, posPezzi, n, i+1, i-1)%1000000007)%1000000007;
}
int taglia(int N, int V[])
{
vector<int> posPezzi(N);
vector<int> temp(1000007, -1);
for(int i=0;i<N;++i){ //con questo ciclo memorizzo dentro posPezzi per ogni pezzo la posizione del precedente
posPezzi[i]=temp[V[i]];
temp[V[i]]=i;
}
return recursive(V, posPezzi, N);
}
Praticamente mi salvo in un vettore il numero di soluzioni per ogni ultimo taglio. In questo modo se successivamente dovrò fare lo stesso taglio mi basta restituire il risultato memorizzato. Per esempio se ho l’input:
5
3 1 3 1
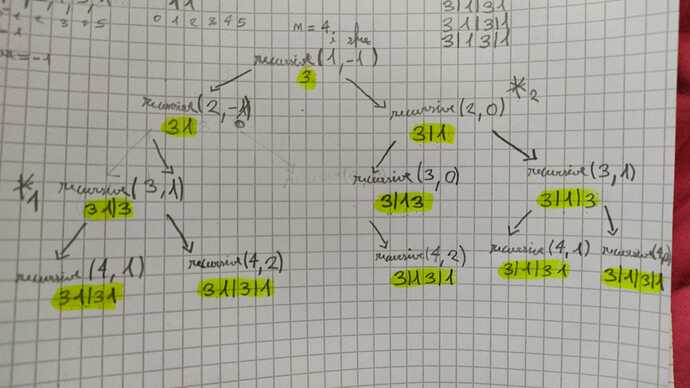
Con l’algoritmo brute force l’albero delle chiamate è questo:
Qui per esempio mi genero tutto l’albero di sinistra di recursive(1, -1), memorizzandomi il risultato di recursive(3, 1) (asterisco 1) e non solo. Quando poi mi trovo in recursive(2, 0) (asterisco 2) e da qui invoco recursive(3, 1) visto che effettuo un taglio dove lo avevo gia fatto sono in grado di restituire immediatamente il risultato in quanto gia calcolato precedentemente.


 .
. ). Per fare un esempio
). Per fare un esempio