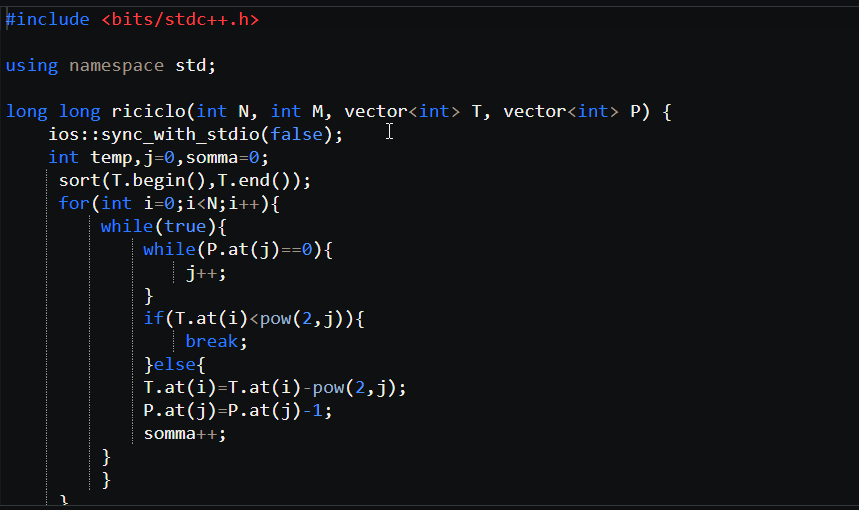
Ciao ragazzi sto svolgendo il problema qui sopra e sto riscontrando parecchi problemi, non sono molto esperto e facendo il submit di questo programma mi viene restituito in molti test error signal 6, che cosa significa ? Inoltre vorrei sapere se fosse possibile vedere gli input nei vari test perché non sapendo quale input causa l’errore si va un po’ alla cieca…
Ecco il codice
Penso che sia accesso a memoria non allocata: molto probabilmente la variabile j accede a una posizione non lecita di P.
Ti consiglio di non usare la funzione pow e di pre-calcolare le potenze di 2. Non solo ottimizzi i tempi ma eviti errori di precisione dovuti ai decimali.
Inoltre, se non conosci come avviene l’input e output del programma, non usare:
ios::sync_with_stdio(false)
potrebbero succedere cose non molto belle soprattutto con problemi interattivi.
P.S
Per postare il codice, basta racchiuderlo tra ```. Una riga sopra il codice, e una riga sotto.
Sono riuscito a risolvere il problema dell’out of range e ho sostituito pow con una funzione creata da me, solo che quando sottometto il problema ci mette troppo a eseguirsi e alcuni output non sono coretti dandomi 5/100 se hai qualche idea per ottimizzarlo e dirmi dove sto sbagliando mi saresti di grande aiuto
#include <bits/stdc++.h>
using namespace std;
long long binpow(long long a, long long b) {
long long res = 1;
while (b > 0) {
if (b & 1)
res = res * a;
a = a * a;
b >>= 1;
}
return res;
}
long long riciclo(int N, int M, vector<int> T, vector<int> P) {
long long int temp,j=0,somma=0;
sort(T.begin(),T.end());
for(long long int i=0;i<N;i++){
while(true){
while(P.at(j)==0){
if((P.back()==0)&&(j==M-1)){
break;
}else{
j++;
}
}
if((P.back()==0)&&(j==M-1)){
break;
}
if(T.at(i)<binpow(2,j)){
break;
}else{
T.at(i)=T.at(i)-binpow(2,j);
P.at(j)=P.at(j)-1;
somma++;
}
}
if((P.back()==0)&&(j==M-1)){
break;
}
}
return somma;
}
Non ho troppa voglia di stare a guardare al codice quindi non ti rispondo alle domande che hai fatto, pero’ ti posso dire che 2^k lo puoi calcolare con 1ll<<k se sta in 64 bit.