DFS Tree
Prerequisiti
- Depth-First Search
Introduzione
L’intero post è riadattato da qui. Avendo trovato molto interessante il blog su Codeforces ho pensato di riproporlo in italiano per renderlo più accessibile. Verranno presentati alcuni usi del DFS Tree per risolvere problemi che altrimenti potrebbero risultare tediosi da scrivere. Inoltre, il meccanismo dietro queste soluzioni non è solo facile da implementare, ma anche estremamente facile da capire e può dare una prospettiva più chiara sul problema.
Il DFS Tree
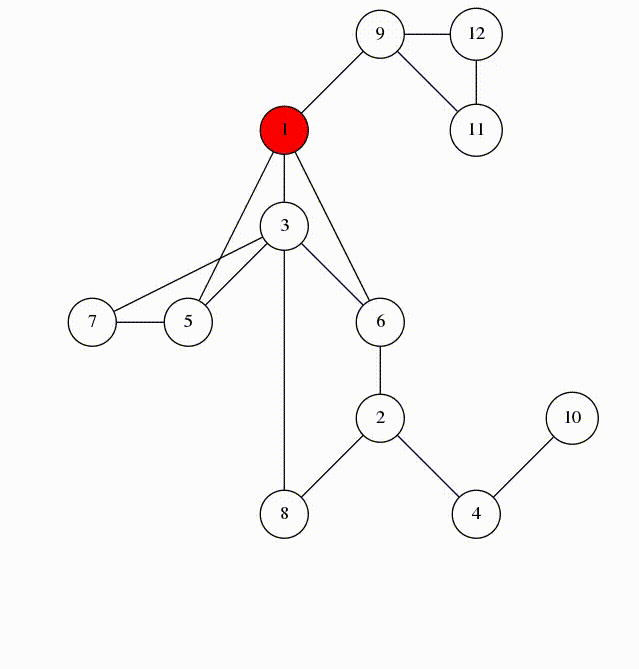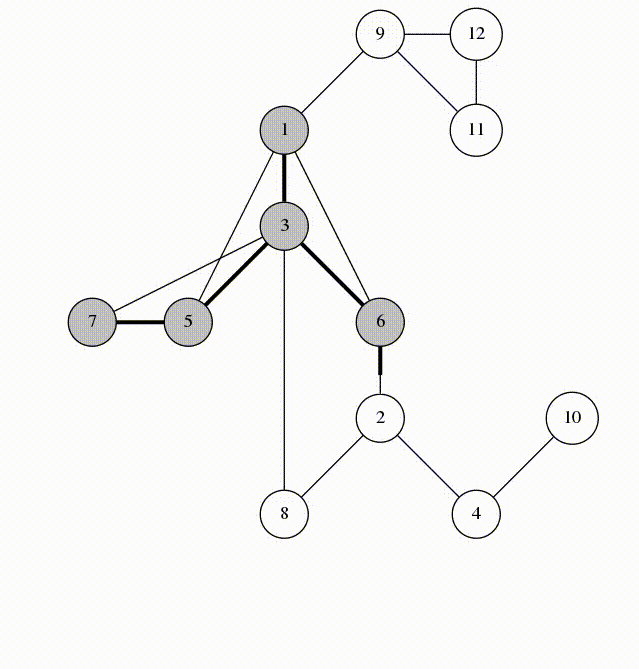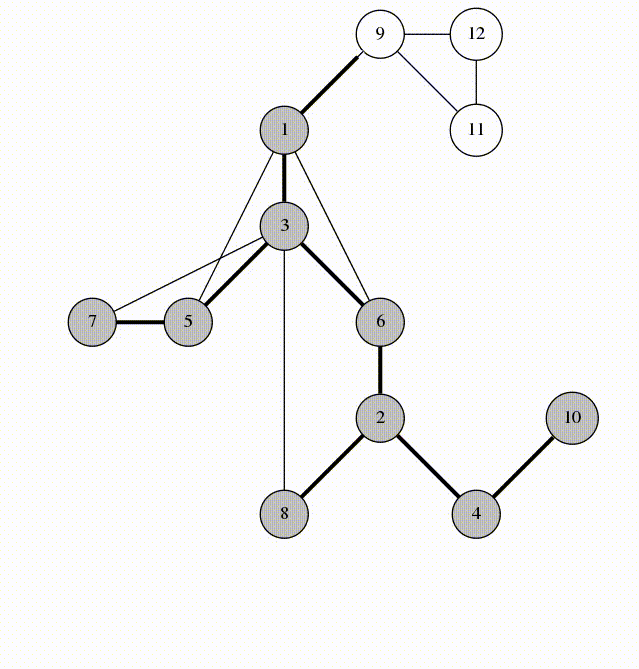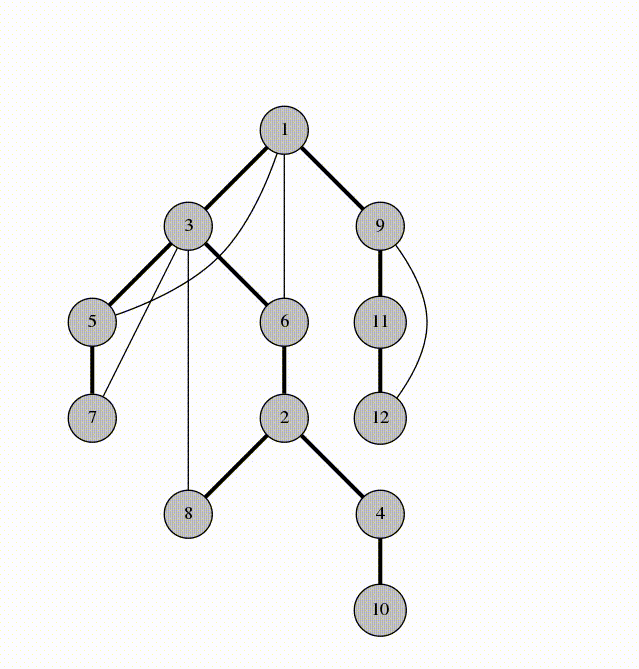
Supponiamo di avere un grafo non diretto e connesso G, con N nodi e M archi. Eseguiamo ora una DFS del grafo, partendo dal nodo in cui vogliamo ancorare il DFS tree. Ogni volta che percorriamo un arco, se porta a un nodo già visitato, lo contrassegnamo come “Span Edge”, ovvero un arco che appartiene al DFS tree.
Ogni arco che non è uno span edge viene detto “Back Edge”.
In C++, la funzione sarà simile a:
bool visitato[N]; // usato per sapere se un nodo è già stato visitato
bool span_edges[M]; // gli span edges avranno valore "true", i back "edges false"
vector<pair<int,int>> adj[N]; // liste di adiacenza del grafo, ogni pair sarà del tipo {nodo a cui porta, indice dell'arco}
void dfs(int nodo){
visitato[nodo] = true;
for(auto x: adj[nodo]){
if(visitato[x.first])continue; //non dobbiamo processare due volte uno stesso nodo
span_edge[x.second] = true;
dfs(x.first);
}
}
Possiamo fare alcune osservazioni, estremamente facili da verificare:
-
Gli span edges formano un albero, difatti sono N-1 poichè viene aggiunto uno span edge ogni prima volta che un nodo diverso dalla radice viene visitato e ogni nodo viene visitato, essendo G connesso.
-
Tutti i back edges connettono un nodo a un suo ancestor o discendente nel DFS tree. Supponiamo che esista un arco ab tale che a non sia un discendente o un ancestor di b. Supponiamo inoltre, senza perdita di generalità, che a venga visitato prima di b. Quando viene processato l’arco ab: se b non è ancora stato visitato, ab è uno span edge, altrimenti, poichè dfs(b) è stata chiamata dopo dfs(a) ma prima della sua conclusione, b appartiene al sottoalbero di a e ne è quindi discendente.
Abbiamo raggiunto un assurdo, quindi ogni arco nel nostro albero connette due nodi che sono uno discendente dell’altro.
Questa è un’ animazione di come agisce la DFS, gli span edges vengono segnati in grassetto.
Trovare i ponti con il DFS tree
In un grafo indiretto connesso, un ponte è un arco la quale rimozione renderebbe il grafo non connesso.
Una volta costruito il DFS tree, quali possono essere i ponti?
Osservazione 1
Un back edge non può essere un ponte, infatti connette nodi già connessi da uno o più span edges.
Osservazione 2
Uno span edge è un ponte se e solo se non ci sono back edges che connettono un suo discendente a un suo ancestor.
Dunque, come capire se un nodo non ha back edges che vi “passano sopra”?
Si può usare la programmazione dinamica sull’albero, considerando per ogni nodo il numero di back edges che partono da un suo discendente e arrivano a un suo predecessore.
Se dp[i]=0, allora l’arco che connette i a suo padre è un ponte.
Questa dp è facilmente calcolabile. In C++, il codice può essere scritto come:
vector<int> ponti; // salviamo in questo vettore i nodi i tali che dp[i]=0
bool visitato2[N];
int dp[N];
void trova_ponti(int nodo){
visitato2[nodo] = 1;
for(auto x: adj[i]){
if(!span_edge[x.second]){
if(visitato2[x.first])dp[nodo]++; //i nodi già visitati sono predecessori
else dp[nodo]--; //quelli non visitati discendenti
}else{
if(!visitato2[x.first]){
trova_ponti(x.first);
dp[nodo]+=dp[x.first];
}
}
}
if(dp[nodo]==0)ponti.push_back(nodo);
}
Per ogni nodo, dp[i] può essere calcolato come somma di dp fra i suoi figli, a cui va aggiunto il numero di back edges che connettono i a un suo ancestor e sottratto il numero di quelli che portano a un suo discendente.
Processare i cactus con il DFS tree
Un cactus è un grafo indiretto connesso in cui ogni nodo appartiene a al più un ciclo.
Per trattare questo tipo di grafo è spesso utile comprimere tutti i nodi appartenenti allo stesso ciclo in un unico nodo.
Il DFS tree consente di eseguire questa operazione molto comodamente:
Poichè ogni nodo può appartener ad al più un ciclo, ci sarà al più un back edge che passa sopra ogni nodo. Inoltre, tutti i nodi sotto lo stesso back edge appartengono allo stesso ciclo e se su un nodo non passano back edges, esso non appartiene ad alcun ciclo.
Problemi correlati
Problemi che possono essere risolti usando il DFS tree, su codeforces.
231 E
858 F
1325 F