Ois velox @ 10 / 100

ElephanZ · 4 Maggio 2018, 7:52pm

Salve a tutti,
Oggi ho provato a risolvere il problema “velox” delle ois2014.
Ottengo solo 10 punti, anche se sono quasi certo che la soluzione sia corretta… vorrei più che altro capire se è un problema di codice o se proprio la mia idea è sbagliata…
Qui c’è il mio codice {https://pastebin.com/0QnEuwT1}.
Grazie

bortoz · 5 Maggio 2018, 2:33pm

Ciao, un esempio in cui il tuo programma sbaglia è il seguente:

Il percorso ottimale è 1-2-3 e quindi la risposta è 2, ma il tuo programma stampa 1.

ElephanZ · 22 Ottobre 2018, 7:34pm

Con questo nuovo codice (https://pastebin.com/WRgDx6Tu) ottengo sempre 10/100 e il tuo esempio funziona correttamente.
Cosa mi consigli ?

zJack1342 · 22 Ottobre 2018, 8:18pm

Devi affidarti alla programmazione dinamica.
Utilizzare il primo arco con velocità strettamente crescente a quella precedente che ti porta a un nodo non visitato non è sempre conveniente.

Output 3 e non 2.

ElephanZ · 25 Ottobre 2018, 4:08pm

Onestamente sono proprio a mare con la programmazione dinamica. Non la capisco proprio…
Mi aiuteresti ad entrare nella logica della DP con questo esercizio?

zJack1342 · 25 Ottobre 2018, 5:11pm

Non sei l’unico xD Anch’io ho grandi difficoltà in questa tipologia di problemi.
Iniziare da velox per introdurre la programmazione dinamica per me è difficile come cosa, visto che ho usato un approccio abbastanza inusuale per risolverlo.
La programmazione dinamica consiste nel trovare la soluzione ottimale di un problema combinando le soluzioni ottimali dei sottoproblemi relativi ad esso.
Prendendo in considerazione velox in cui ci è richiesto di trovare il traggito più lungo con archi strettamente maggiori, il problema più grande è il traggitto completo mentre il relativo sottoproblema è il traggito più lungo relativo a un determinato arco.
Il sottoproblema del arco si ripete per ogni sua adiacenza e il problema relativo a ogni adiacenza si ripeterà per le adiacenze relative ad esso fin quando non potrai più usfruire di archi.
Il vantaggio della programmazione dinamica è proprio questo, combinare risultati già ottenuti senza doverli ricalcolare per ottenere il migliore.
Le difficoltà di questa tipologia sono molteplici, come trovare la struttura dati che contenga i risultati dei vari sottoproblemi e come ricavare tali soluzioni.
Esistono due approcci per risolvere questi problemi, top down e bottomup.
La top down (ricorsione) scompone il problema più grande in probelmi più piccoli facilmente risolvibili mentre la bottomup (iterativa) risolve problemi più piccoli per poi arrivare a quello più grande.
L’ apporccio da scegliere dipende soprattutto da come si ragiona e dalla natura del problema.
Io inizierei col risolvere i classici come poldo , sommelier e discesa massima. Per poi provare problemi semplici come number game , convegno aziendale e medaglie.
Credo di non essere stato chiarissimo ma ho fatto il meglio che potessi fare.
Se un utente più esperto ci vuole dare una mano ben vegna, ho solo da imparare.

ElephanZ · 25 Ottobre 2018, 5:16pm

Grazie, apprezzo molto il tuo impegno nel cercare di introdurmi un argomento abbastanza complicato

frakkiobello · 21 Giugno 2019, 3:37pm

Voglio proporre una soluzione alternativa per questo problema, in questo contesto non è la migliore ma secondo me può tornare utile per altri problemi.

L’idea è di partire dalla dp top-down che prova ricorsivamente ogni soluzione possibile e migliorarla fino a farla stare nel tempo limite.

Top Down base: Lo stato della dp sarebbe (Nodo, Velocità) dove Nodo rappresenta il nodo a cui siamo arrivati mentre Velocità rappresenta la velocità dell’ultimo arco, ossia la massima sino ad ora. Basta dunque lanciare la funzione su ogni nodo e mantenere la massima:
Questa soluzione è sicuramente troppo lenta.

   int res=0;
   for(auto near:g[node])	//Per ogni vicino 
   	if(near.first>speed)	//Controllo che la velocità sia sufficiente 
   		res=max(res,1+dp(near.second,near.first));	//Aggiorno il risultato
   return res;
}
for(int i=0;i<n;i++) res=max(res,dp(i,-1));

Memoizzazione: È possibile che durante l’esecuzione dell’algoritmo uno stato sia ricalcolato più volte e dunque anche tutte le funzioni che vengono chiamate nel suo albero ricorsivo. È possibile memorizzare i vari stati in modo da non ricalcolarli, ma la soluzione rimane sia troppo lenta ma soprattutto gli stati diversi , ora, sono troppi per essere memorizzati.

map<pair<int,int>,int> memo;
int dp(int node, int speed){
	if(memo.find({node,speed})!=memo.end())
		return memo[{node,speed}];
	int res=0;
	for(auto near:g[node])	//Per ogni vicino 
		if(near.first>speed)	//Controllo che la velocità sia sufficiente 
			res=max(res,1+dp(near.second,near.first));	//Aggiorno il risultato
	return memo[{node,speed}]=res;
}

Riduzione degli stati: come detto in precedenza il numero degli stati è attualmente troppo elevato, sia per essere memorizzati sia per essere calcolati, eppure molto stati compiono le medesime istruzioni:

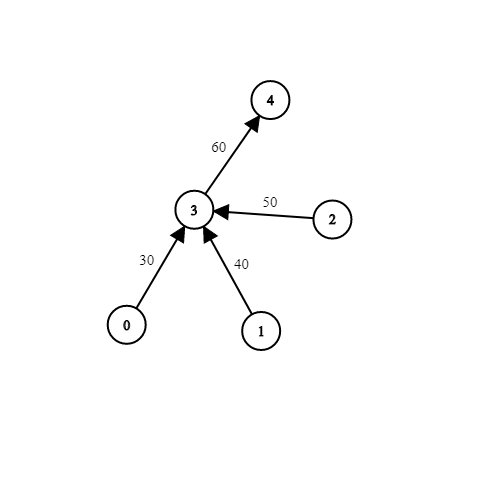
Come è possibile vedere bene in questo caso, arrivando al nodo 3 arrivando dai nodi 0, 1, 2 si generano 3 stati differenti, quando in realtà dp(3,30), dp(3,40), dp(3,50), verranno trattati nello stesso modo. Quello che ci interessa veramente non è la velocità con cui arriviamo ma quanti archi uscenti dal nodo 3 non posso prendere perché troppo lenti. Gli stati sono dunque: dp(3,0), dp(3,0), dp(3,0), in questo modo verranno calcolati una sola volta.
Come trovare il secondo parametro della dp: Il modo più semplice per farlo è: controllo quanti archi del nodo in cui sto andando hanno una velocità minore o uguale a quella dell’arco con cui ci sto andando, questo algoritmo però si dimostra essere troppo lento, in quanto gli archi uscenti da un nodo potrebbero essere molti.
Come trovare velocemente il secondo parametro della dp: Innanzitutto procediamo ordinando tutti gli archi uscenti da ogni nodo in base alla loro velocità, fatto ciò possiamo utilizzare la ricerca binaria per trovare il secondo parametro molto velocemente.

for(int i=0;i<n;i++)
	if(!g[i].empty())
		sort(g[i].begin(), g[i].end());

map<pair<int,int>,int> memo;
int bs(int node, int limit){
	if(g[node].empty()) return 1e9;
	int low=0, high=g[node].size()-1, mid, res=g[node].size();
	while(low<=high){
		mid=(low+high)/2;
		if(g[node][mid].first>=limit){
			res=mid;
			high=mid-1;
		}
		else low=mid+1;
	}	
	return res;
}
int dp(int node, int skip){
	if(skip>=g[node].size() || g[node].empty()) return 0;
	if(memo.find({node,skip})!=memo.end()) return memo[{node,skip}];
	int res=0;
	for(int i=skip;i<g[node].size();i++){
		int speed=bs(g[node][i].second,g[node][i].first+1);
		res=max(res,1+dp(g[node][i].second,speed));
	}
	memo[{node,skip}]=res;
	return res;
}

In questo modo la soluzione rimane nel tempo limite senza troppi problemi.

Numero degli stati: Il numero di stati corrisponde a: \sum_{i=0}^n g[i].size() quindi al numero totale di archi ossia m che è un numero di stati drasticamente inferiore alla soluzione iniziale.
Memoizzazione più efficace: Questo punto non è sicuramente necessario ma aumenta comunque l’efficienza della soluzione: Essendo il numero di stati uguali al numero di archi possiamo trovare un modo per memorizzare ogni stato evitando di scomodare mappe che rallentano la soluzione:
7.1. : Utilizzare un vector<vector<int>> memo facendo in modo che memo[i].resize(g[i].size())
7.2: Si possono effettuare le somme prefisse sui gradi dei nodi in ordine in modo che per ogni i: prefix[j+1] contenga \sum_{i=0}^j g[i].size() ossia il numero di archi uscenti dai nodi con indice inferiore a quello in questione. A questo punto lo stato che prima era [nodo, skip] può diventare [startingPoint] dove startingPoint=prefix[node]+skip quindi monodimensionale, avendo dunque la possibilità di usare un array come memo. Questa soluzione è sicuramente troppo complicata in quanto serve poi un altro array per capire a quale nodo e a quale arco risponde startingPoint. Nonstante ciò funziona anch’essa in tempo costante.

Fabio.

bortoz · 22 Giugno 2019, 7:28am

Ho un dubbio: al punto 2 lo stato è (nodo, velocità) ma per ogni nodo il numero di velocità distinte con cui si può entrare è nel caso peggiore uguale al numero di archi entranti, quindi il numero di stati di un nodo dipende dal grado (del grafo rovescio) del nodo e il numero totale di stati è la somma dei gradi dei nodi che è \mathcal O(M). È corretto ciò o mi sono perso qualcosa per strada?

frakkiobello · 22 Giugno 2019, 7:51am

In realtà hai pienamente ragione, tant’è vero che passa anche in quel modo, a mia discolpa posso però dire che funziona per questo esercizio in particolare ma se la condizione di un passaggio da un nodo all’altro fosse stata diversa avrebbe potuto non funzionare.

Il punto è che l’obiettivo è rendere lo stato dipendente solamente dal nodo attuale in modo che il numero di stati sia limitato, poi ribadisco che in questo contesto il numero di stati non cambia però l’algoritmo proposto è più versatile.