Introduzione ai Segment Tree
Visti i numerosi thread comparsi recentemente nel forum riguardo problemi con i segment tree, ho provato a scrivere questa breve introduzione a una delle strutture dati più “famose” nell’ambito della programmazione competitiva. Se ci fossero errori, impercisioni o punti spiegati male, fatemelo sapere, grazie.
Prerequisiti
- conoscenza di base sugli alberi
- utilizzo di funzioni ricorsive
A cosa serve un segment tree
Partiamo dal considerare il seguente problema: “ci è dato un array A di N interi (N\le10^6) e dobbiamo eseguire Q operazioni (Q\le10^6) che possono essere una query sulla somma del range [l,r[ o modificare l’i-esimo elemento dell’array”
Approccio 1
Query O(N) e update O(1)
La prima idea che viene in mente è implementare le richieste in maniera naive, modificando gli elementi nell’array e sommando quelli gli interi di un range con un ciclo for. Ci si accorge presto che questa soluzione risulta troppo lenta. Il caso pessimo (se tutte le operazioni fossero query di somma sull’intero l’array) verrebbero eseguite circa 10^{12} operazioni; ben oltre quello che ci serve per non fare TLE.
Approccio 2
Query O(1) e update O(N)
Un approccio più sofisticato ma comunque inefficiente è precalcolare le somme prefisse dell’array in modo da poter rispondere velocemente alle query di somma. Tuttavia modificare un elemento comporta la modifica di tutte le somme prefisse dalla posizione dell’elemento in poi. Il caso pessimo (solo update sul primo elemento) ha la stessa complessità del precedente approccio, di conseguenza anche questo si rivela poco efficace.
Approccio 3
Query O(\log_{2}N) e update O(\log_{2}N)
L’approccio migliore per questo tipo di problema è utilizzare il segment tree. Si tratta di una struttura dati molto utilizzata quando si tratta di eseguire query e update su un array. Le operazioni possono essere eseguite sia su un solo elemento (point update/point query) che su range di elementi contigui (range update/rangequery). Ciascuna di queste operazioni, siano esse su range o singoli elementi, avranno complessità O(\log_{2}N).
Il problema descritto sopra richiede point update e range sum.
I segment tree
Idea: Posso evitare di iterare su tutti gli elementi?
Un’idea che può venire in mente è di salvarsi la somma di alcuni dei range per non doverli ricalcolare da capo ogni volta. Se questa cosa viene fatta in maniera corretta può portare a un significativo miglioramento delle performance. Per quanto riguarda gli update, vorremmo anche fare in modo di non dover modificare troppi “range precalcolati”. Spesso la cosa migliore per massimizzare l’efficienza è trovare un compromesso tra query e update.
Come è fatto un segment tree?
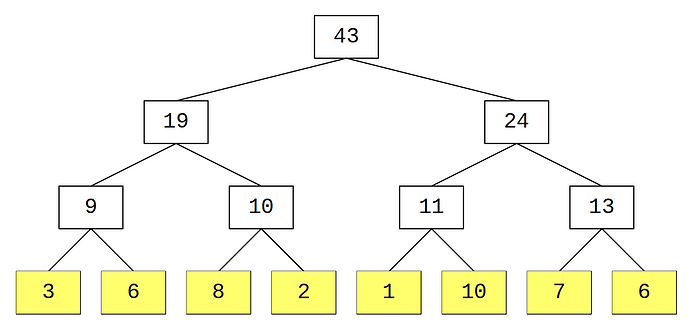
Il modo migliore di capire come è fatto un segment tree è vederne una rappresentazione schematica:
Gli elementi in giallo sono quelli dell’array originale e ogni altro nodo contiene la somma dei due nodi sottostanti.
Qualche osservazione
- Se la dimensione dell’array iniziale è N, ci serviranno N+N/2+N/4+N/2^k+...+1 \approx 2N nodi.
- La profondità di un path dalla radice a ciascuna delle foglie è O(\log_{2}N).
- Ciascun nodo contiene la somma delle foglie del suo sottoalbero, che corrisponde a un sottoarray di lunghezza 2^k dell’array originale.
Vediamo nel dettaglio come avvengono le varie operazioni.
Update
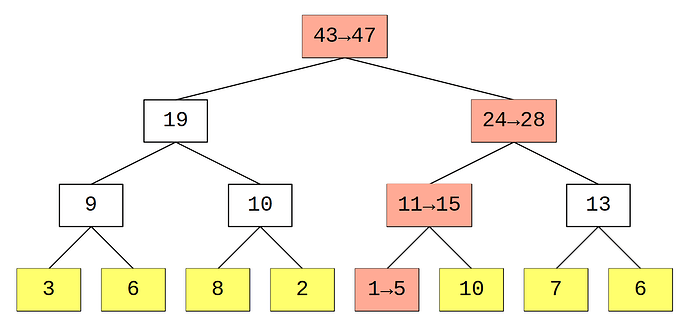
Se vogliamo modificare l’i-esimo elemento ci accorgiamo che i nodi del segment tree da aggiornare sono solo quelli del path dalla radice all’i-esima foglia. E siccome la profondità dell’albero è \log_{2}N, la complessità dell’update sarà per l’appunto O(\log_{2}N).
I nodi evidenziati in rosa sono quelli interessati dall’update, in questo caso è stato cambiato il quinto elemento, che è diventato 5, e il valore dei nodi tra la foglia e la radice (compresi) è stato modificato di conseguenza.
Query
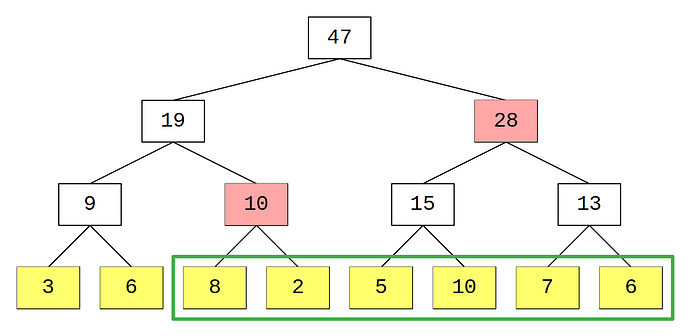
Per quanto riguarda la somma di un range, il nostro obiettivo è non dover iterare su tutti gli elementi del range, ma sfruttare i range di cui conosciamo la somma per “comporre” il range interessato. È facilmente dimostrabile (ma non necessario agli scopi di questa introduzione) che il numero di nodi che compone un range è al più 2\log_{2}N.
Nell’immagine il range della query è composto dagli ultimi 6 elementi nel riquadro verde ma notiamo che bastano i due nodi evidenziati in rosso per ottere la somma richiesta.
Implementazione
L’albero
I segment tree sono di fatto alberi binari completi e profondi \log_{2}N. Di conseguenza è possibile memorizzarli all’interno di un singolo array lungo \approx 2N. Tuttavia, siccome l’array non è sempre lungo una potenza di due, possiamo utilizzare un array lungo 4N ed essere sicuri che vada bene per qualsiasi N.
In questa implementazione il segment tree è 1-based, cioè la radice si trova in posizione 1 dell’array. Prendendo in considerazione il nodo i-esimo, il suo figlio sinistro sarà in posizione 2i e il destro in posizione 2i+1. Il padre del nodo i sarà in posizione \lfloor i/2 \rfloor.
Per semplicità implementativa, è bene scrivere una classe (o struct) segtree per mantenere ordine e facilitare l’eventuale debugging.
typedef long long ll; // sempre meglio usare i long long
struct segtree {
int N; // simensione dell'array originale
vector<ll> st; // array in cui memorizziamo l'albero
};
build
Complessità: O(N)
Il costruttore della classe riceve l’array su cui vorremo effettuare le operazioni e ridimensiona l’array del segment tree a 4N.
segtree (vector<ll> &A) {
N = A.size();
st.resize (4*N); // 4N va sempre bene
build(1,0,N,A);
}
Successivamente chiama la funzione ricorsiva build che costruisce ricorsivamente il segment tree.
ll build (int i, int left, int right, vector<ll> &A) {
// funzione ricorsiva che costruisce un range del segment tree e restituisce la somma del range
if (right - left == 1) { // caso base
// il nodo si riferisce a un solo elemento
return st[i] = A[left];
}
// divido a metà il range e costruisco ricorsivamente
int mid = (left + right) / 2;
st[i] = build(2*i, left, mid, A) +
build(2*i+1, mid, right, A);
// restituisco la somma di questo range
return st[i];
}
La costruzione ricorsiva prende come parametri l’indice i del nodo del segment tree, gli estremi left (incluso) e right (escluso) del range [left,right[ che stiamo costruendo. Il range si riferisce all’array di interi su cui facciamo le operazioni. Ciò significa che il nodo i conterrà la somma del range [left,right[ di A. L’ultimo parametro è infatti l’array A, che è importante passare per riferimento, evitando di generarne una copia ad ogni chiamata.
Caso base: il range è lungo 1, cioè contine la somma di un solo elemento di A (cioè A[left]), possiamo quindi assegnare il valore e restituirlo.
Caso generale: dividiamo a metà il range e costruiamo ricorsivamente le due metà. Il valore del nodo sarà quindi la somma dei due range in cui l’abbiamo diviso (i valori restituiti dalle chiamate ricorsive).
Per dividere un range a metà troviamo il punto medio mid facendo la media (approssimata per difetto) di left e right. La posizione mid sarà il primo elemento della metà a destra. La metà sinistra ricorre sul range [left,mid[ mentre quella destra su [mid,right[.
update
Complessità: O(log_{2}N)
Anche l’update avviene con una funzione ricorsiva. Un dettaglio che può semplificare il successivo utilizzo del segment tree è scrivere una procedura che viene chiamata dall’esterno con due soli parametri (posizione e nuovo valore) la quale chiama una procedura omonima interna con tutti i parametri necessari.
void update (int i, int left, int right, int pos, ll val) {
// funzione ricorsiva che modifica il valore di un elemento e tutti i nodi interessati
if (right - left == 1) {
// caso base
st[i] = val;
return;
}
// ricorro sulla metà in cui si trova l'elemento da modificare
int mid = (left + right) / 2;
if (pos < mid) { // sta nella metà sinistra
update (2*i, left, mid, pos, val);
} else { // sta a destra
update (2*i+1, mid, right, pos, val);
}
// aggiorno il valore del nodo come somma dei figli
st[i] = st[2*i] + st[2*i+1];
}
void update (int pos, ll val) {
update (1, 0, N, pos, val);
}
I parametri sono gli stessi della funzione build ma al posto dell’array abbiamo pos che indica l’indice dell’elemento che vogliamo modificare e val, cioè il nuovo valore.
Il caso base è sempre il range lungo 1: se il nodo si riferisce a un solo elemento (quello che vogliamo modificare), cambiamo il suo valore.
Nel caso generale dividiamo sempre a metà il range ma al posto di ricorrere su entrambi i figli, ricorriamo sul sinistro se l’elemento da modificare sta nella prima metà. Sul destro altrimenti.
Dopo la chiamata ricorsiva aggiorniamo il valore del nodo facendo la somma dei valori dei figli (uno dei quali sarà stato modificato dall’update).
query
Complessità: O(log_{2}N)
Le query su un range hanno una struttura leggermente diversa ed è meno intuitivo il motivo per cui la complessità rimane logaritmica. Accenno una possibile dimostrazione (non formale) che può benissimo essere ignorata.
Molto vagamente
Supponiamo che la funzione ricorra sulle due metà e che nessuna delle due sia un caso base. A questo punto entrambi i range avranno sempre uno dei due estremi inclusi nel range della query e di conseguenza da quel momento in poi ad ogni chiamata una delle due metà arriva a un caso base. Se mid non è incluso nel range della query allora una delle due metà avrà intersezione nulla, contrariamente uno dei due range è totalmente incluso. Possiamo concludere che può accadere solo una volta che entrambi i range su cui ricorre non siano casi base e di conseguenza la complessità è O(\approx 4\log_{2}N) che equivale a O(log_{2}N).
ll query (int i, int left, int right, int query_left, int query_right) {
// funzione ricorsiva che restituisce la somma del range [query_left,query_right[
if (query_left >= right || query_right <= left) {
// caso base 1
// il range del nodo non ha intersezioni con il range della query
return 0;
}
if (left >= query_left && right <= query_right) {
// caso base 2
// il range del nodo è totalmente incluso nel range della query
return st[i];
}
// ricorro sulle due metà
int mid = (left + right) / 2;
return query (2*i, left, mid, query_left, query_right)+
query (2*i+1, mid, right, query_left, query_right);
}
ll query (int query_left, int query_right) {
return query (1, 0, N, query_left, query_right);
}
La funzione query a differenza delle precedenti ha due casi base:
- il range del nodo non ha intersezioni con quello della query, quindi la somma dell’intersezione è 0
- il range del nodo interseca totalmente quello della query, quindi ritorno la somma del range
Nel caso generale ricorro sulle due metà senza modificare query_left e query_right dato che il range della query rimane sempre lo stesso.
Implementazione completa
Implementazione in C++
struct segtree {
int N;
vector<ll> st;
ll build (int i, int left, int right, vector<ll> &A) {
if (right - left == 1) {
return st[i] = A[left];
}
int mid = (left + right) / 2;
st[i] = build(2*i, left, mid, A) +
build(2*i+1, mid, right, A);
return st[i];
}
segtree (vector<ll> &A) {
N = A.size();
st.resize (4*N);
build(1,0,N,A);
}
void update (int i, int left, int right, int pos, ll val) {
if (right - left == 1) {
st[i] = val;
return;
}
int mid = (left + right) / 2;
if (pos < mid) {
update (2*i, left, mid, pos, val);
} else {
update (2*i+1, mid, right, pos, val);
}
st[i] = st[2*i] + st[2*i+1];
}
void update (int pos, ll val) {
update (1, 0, N, pos, val);
}
ll query (int i, int left, int right, int query_left, int query_right) {
if (query_left >= right || query_right <= left) {
return 0;
}
if (left >= query_left && right <= query_right) {
return st[i];
}
int mid = (left + right) / 2;
return query (2*i, left, mid, query_left, query_right)+
query (2*i+1, mid, right, query_left, query_right);
}
ll query (int query_left, int query_right) {
return query (1, 0, N, query_left, query_right);
}
};
Quando si può usare un segment tree
I segment tree sono quasi sempre una buona scelta quando si tratta di fare update e query su range, ma non vanno bene per tutte le operazioni. In particolare funzionano con le operazioni dette associative come il minimo/massimo, lo XOR, il prodotto, il GCD etc.
Se per esempio ci interessasse il massimo in un range al posto della somma, al posto di unire i due figli di un nodo facendone la somma, si prende il massimo dei due.
st[i] = max(st[2*i], st[2*i+1]);
I segment tree permettono anche di eseguire operazioni più complesse come trovare il subarray di somma massima in un range, trovare il k-esimo elemento (salvando le frequenze) o trovare il primo elemento \ge k in range.
Versioni più elaborate permettono di eseguire query su versioni precedenti della struttura (persistenti) o di memorizzare valori in range più ampi (segment tree sparsi)… gli utilizzi sono innumerevoli.
Il tipo di segment tree spiegato in questa introduzione permette di eseguire point update/range query oppure point query/range update ma con una tecnica chiamata Lazy Propagation è possibile supportare range query/range update.