Cerco di spiegarmi meglio:
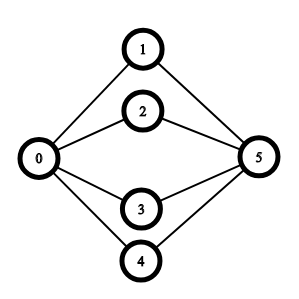
Partiamo utilizzando l’algoritmo che avevi scritto tu sul grafo che ho postato io:
Nodo di partenza il nodo 0, quello di arrivo il nodo 5.
coda:0, visitati:
Togli lo 0 , coda: e lo visiti visitati:0 Iteri sui vicini dello 0:
Nodo 1, non è stato visitato allora lo inserisci nella coda coda:1
Nodo 2, non è stato visitato allora lo inserisci nella coda coda:1,2
Nodo 3, non è stato visitato allora lo inserisci nella coda coda:1,2,3
Nodo 4, non è stato visitato allora lo inserisci nella coda coda:1,2,3,4
Togli l’1 e lo visiti coda:2,3,4, visitati:0,1 Iteri sul vicini dell’1
Nodo 0, è stato visitato, quindi non fai nulla.
Nodo 5, non è stato visitato quindi lo inserisci in coda coda:2,3,4,5
Togli il 2 e lo visiti coda:3,4,5,, visitati:0,1,2 Iteri sul vicini dell’2
Nodo 0, è stato visitato, quindi non fai nulla.
Nodo 5, non è stato visitato quindi lo inserisci in coda coda: 3,4,5,5
Togli il 3 e lo visiti coda:4,5,5, visitati:0,1,2,5 Iteri sul vicini dell’3
Nodo 0, è stato visitato, quindi non fai nulla.
Nodo 5, non è stato visitato quindi lo inserisci in coda coda: 4,5,5,5
Togli il 4 e lo visiti coda:5,5,5,, visitati:0,1,2,3,4 Iteri sul vicini dell’4
Nodo 0, è stato visitato, quindi non fai nulla.
Nodo 5, non è stato visitato quindi lo inserisci in coda coda: 5,5,5,5
Già qui ti accorgi che nella coda hai 4 volte lo stesso nodo ed è sicuramente uno speco di tempo, considerando che in questo piccolo esempio sono 4 le occorrenze ma aumentando il numero di nodi collegati tra 0 e 5 aumenterebbero anche le occorrenze del 5 nella coda.
La miglioria che ti avevo proposto consiste nel settare il nodo 5(ovviamente anche gli altri nodi) visitati nel momento in cui li inserisci nella coda.
In questo modo quando arrivavi al nodo 2 e trovavi come vicino il 5, vedendo che è già stato visitato eviti di inserirlo nuovamente.
Spero di essermi spiegato meglio.
Fabio.