Excellent2, perche' funziona?

Aiuto
1

ciao a tutti,
ho risolto il problema senza pero’ capire il perche’ la mia soluzione funzioni. La mia idea e’ stata la seguente:

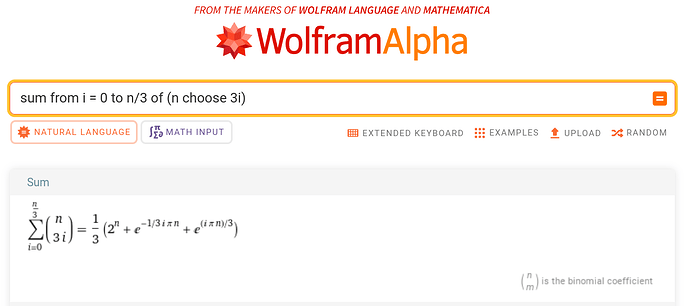
Nel caso in cui n % 3 == 0 il numero di occorrenze di 1 e di 5 deve essere per entrambi un multiplo di 3. Se indico con x le occorrenze di 1(avrei potuto scegliere anche 5) per ogni coppia di occorrenze dovro’ calcolare tutte le permutazioni con la formula {N\choose x}. Le coppie saranno le seguenti: (0, n), (3, n - 3), (6, n - 6)…(n - 3, 3), (n, 0) . Mettendo la formula su wolfram ho ottenuto questa soluzione:

image
image1213×539 36.4 KB

Dato che \sum_{i=0}^{n} {n\choose i} = 2^n mi aspettavo una soluzione che avesse il termine 2^n. La parte reale dei due termini esponenziali \in [-1, 1], quindi facendo qualche if si riesce ad arrivare a una soluzione. Per quanto riguarda n % 3 != 0 si puo’ fare un ragionamento analogo, utilizzando la soluzione data da wolfram di \sum_{i=0}^{n/3} {n\choose 3i+1} e \sum_{i=0}^{n/3} {n\choose 3i+2}. La cosa che non riesco a capire e’ perche’ \sum_{i=0}^{n/3} {n\choose 3i} \simeq 2^n/3. Per caso avrei dovuto vedere questo problema dal punto di vista di: circa un terzo dei numeri composti solamente da 1 e 5 e’ divisibile per 3? A posteriori noto questo, ma non mi sembra qualcosa di intuitivo che mi avrebbe potuto guidare verso la soluzione.
grazie dario :+1:

2

Per avere tutte le combinazioni di 1 e 5 in un numero di N cifre e divisibile per 3 si deve avere:
se N \mod 3 = 0: (0, N), (3,N-3), (6,N-6) …
se N \mod 3 = 1: (2,N-2), (5,N-5), (8,N-8) …
se N \mod 3 = 2: (1,N-1), (4,N-4), (7,N-7) …
Sommando i rispettivi coefficienti binomiali: N \choose 0 + N \choose 3 + N \choose 6 … + N \choose N, oppure N \choose 2 + N \choose 5 + N \choose 8 … + N \choose N-2 oppure N \choose 1 + N \choose 4 + N \choose 7 … + N \choose N-1 ottieni il risultato cercato, ma in questo modo va in time out con N = 10^{18}.
Osservando il triangolo di Tartaglia dei coefficienti binomiali e con alcuni semplici passaggi algebrici, sapendo che:

{\sum_{k = 0}^N} {N \choose k} = 2^N

se N dispari: N \choose 0 + N \choose 3 + N \choose 6 + … + N \choose N = (2^N-2) \over 3

se N pari: N \choose 0 + N \choose 3 + N \choose 6 + … + N \choose N = (2^N+2) \over 3

Gli stessi risultati si ottengono nel caso di resto 1 o 2 con i rispettivi coefficienti binomiali.

3

per passaggi algebrici intendi i calcoli che ti mostrano questo pattern(quindi fare un po’ di prove e ricavarsi questa formula basandosi solo sull’osservazione dei risultati) oppure la formula ottenuta formalmente?