Salve a tutti, negli scorsi giorni ho provato a risolvere il problema lampadine, ma sono riuscito a ottenere solo 60/100, infatti faccio troppe chiamate alla funzione disconnect() per ottenere il punteggio pieno.
Riassumo velocemente il problema:
Abbiamo N lampadine che sono divise in gruppi, le lampadine nello stesso gruppo sono collegate in serie e i vari gruppi sono collegati in parallelo. Dobbiamo identificare i vari gruppi che compongono il circuito, per farlo possiamo utilizzare la funzione disconnect() per scollegare alcune delle lampadine e vedere quali lampadine si accendono nel circuito. Per ottenere 100/100 la funzione disconnect() deve essere invocata al più 10 volte.
Il mio approccio è il seguente. Lavoro con delle coppie (V, max_g) dove l’insieme V è un insieme contenente delle lampadine, mentre max_g è il numero di gruppi massimo in cui possono essere distribuiti tali lampadine. L’idea è di iniziare con la coppia (\{0, 1, \dots, N - 1\}, N) (infatti inizialmente ho N lampadine che possono essere distribuite al più in N gruppi) e con il passare delle iterazioni dividere tale insieme in più sottoinsiemi di dimensione sempre minore. L’idea chiave sta nel fatto che se io (in qualche modo che presenterò successivamente) riuscissi a dividere V in 2 insiemi V_1, V_2 tali che V_1 \cup V_2 = V \land V_1 \cap V_2 = \emptyset e per i quali so non ci sono intersezioni tra i gruppi contenti le lampadine di V_1 e quelle di V_2 allora potrei lavorare su tali insiemi in maniera parallela.
Utilizzando questo spunto vogliamo partire dalla coppia iniziale (\{0, 1, \dots, N - 1\}, N) e scomporla iterativamente in gruppi più piccoli per i quali possiamo capire la suddivisione in gruppi all’interno di essi. Ora spiego come lavoro su un singola coppia (V, max_g) ricordandomi però che poi lavorerò su più coppie contemporaneamente all’interno della stessa iterazione. Il caso base è rappresentato dalle coppie (V, 1), in tal caso so che tutte le lampadine in V appartengono allo stesso gruppo e di conseguenza effettuerò una chiamata a series(V).
Per il caso generico (V, max_g) chiamo disconnect() con \lfloor \frac{max_g}{2} \rfloor lampadine casuali di V e otterrò due insiemi On, Off rispettivamente l’insieme delle lampadine (di V) che rimangono accese e quelle che si spengono con la chiamata a disconnect().
Analizziamo prima l’insieme Off, conterrà tutte le lampadine che abbiamo spento più tutte le lampadine che erano in serie con loro, inoltre sappiamo che tali lampadine saranno divise in al più \lfloor \frac{max_g}{2} \rfloor gruppi (togliendo k lampadine posso spegnere al più k gruppi), otteniamo dunque la coppia (Off, \lfloor \frac{max_g}{2} \rfloor). Vediamo come questa nuova coppia si avvicina al caso base a una velocità sufficiente, infatti dimezzando a ogni iterazione il numero massimo di gruppi richiesti abbiamo un fattore logaritmico che ci permette di suddividere 1000 elementi in 10 iterazioni.
Il collo di bottiglia dell’efficienza del mio ragionamento è dato però dal gruppo On, quindi dalle lampadine che rimangono accese. Infatti (se il gruppo On non è vuoto) possiamo creare la coppia (On, min(max_g - 1, |On|)), nonostante la dimensione di On sia al più la metà di quella di V (quindi qui ho un fattore logaritmico) il nuovo numero massimo di gruppi non decresce abbastanza velocemente. Questo non garantisce che siano sufficienti 10 iterazioni.
Mostro qui un esempio in cui il numero di iterazioni necessarie non risulta logaritmico.
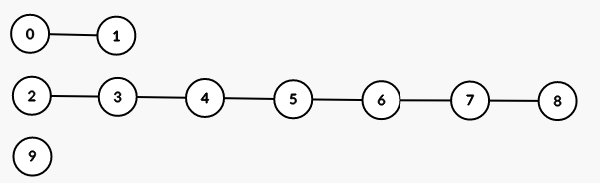
Supponendo di avere questo circuito:
Una possibile simulazione dell’algoritmo potrebbe essere la seguente:
- Coppia iniziale: (\{0, 1, 2, 3, 4, 5, 6, 7, 8, 9\}, 10)
- Iterazione 1:
disconnect({0, 1, 2, 3, 4}), rimane acceso solo la lampadine 9. - Nuove coppie: (\{0, 1, 2, 3, 4, 5, 6, 7, 8\}, 5), (\{9\}, 1)
- Iterazione 2:
disconnect({0, 1}), rimangono accese le lampadine 2, 3, 4,\dots 9 (il gruppo contenente il 9 è già risolto non servono altre query a riguardo) - Le nuove coppie sono quindi: (\{0, 1\}, 2), (\{2, 3, 4, 5, 6, 7, 8\}, 4), (\{9\}, 1), notiamo che però per la seconda coppia ne la cardinalità di V ne max_g sono diminuite logaritmicamente.
Sto sbagliano totalmente approccio oppure devo solo trovare un modo per limitare maggiormente il valore di max_g per l’insieme On?