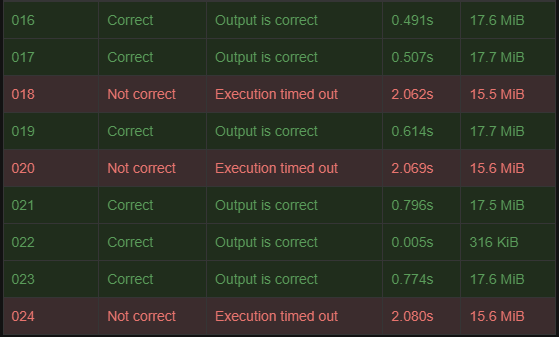
ciao, molto probabilmente ho sbagliato qualcosa di stupido, però ci sto sbattendo la testa e non capisco come è possibile che mi dia gli esempi giusti e tutti gli altri testcase sbagliati. Il ragionamento mi sembra corretto, magari si può ottimizzare qualcosa, però questo è:
ll fastexp(int a, int b){
if (b == 0) return 1;
ll x = fastexp(a, b/2);
if(b % 2 == 0) return (x * x) % mod;
return (x * x * a) % mod;
}
void moltiplica(vector<int> &a, vector<int> &b) {
for(int i = 0; i < a.size(); ++i){
ll x = (b[i] * a[i]) % mod;
b[i] = x;
}
}
void cicla(vector<int> &a, int D){
vector<int> copia(a.size());
for(int i = 0, d = D % a.size(); i < a.size(); ++i, ++d%= a.size()){
copia[d] = a[i];
}
a = copia;
}
vector<int> execute(int n, int k, int d, vector<int> a){
vector<int> b(n, 1);
if(d){
for(int i = 0; i < k%n; ++i){
moltiplica(a, b);
cicla(a, d);
}
int mol = 1;
for(int i = 0; i < n; ++i){
mol = (mol * a[i]) % mod;
}
mol = fastexp(mol, k/n);
for(int i = 0; i < n; ++i){
b[i] = (b[i] * mol) % mod;
}
}else{
for(int i = 0; i < n; ++i){
b[i] = fastexp(a[i], k);
}
}
for(auto &x : b){
x %= mod;
}
return b;
}
int main() {
fast();
int n, k, d; cin>>n>>k>>d;
vector<int> v(n);
for(int i = 0; i < n; ++i){
cin >> v[i];
}
vector<int> sol = execute(n, k, d, v);
for(auto x : sol){
cout << x << " ";
}
return 0;
}
in pratica visto che ciclando il vettore con k > n si incontrano gli stessi numeri moltiplico b per quei numeri moltiplicati insieme e tutto elevato a quanti giri fa k in n (k/n) l’eccesso lo faccio all’inizio.
dove sbaglio?