Help with 'walker'

Olimpiadi
1

Hello. I came up with this formula to calculate the number of all possible paths.
answer = (N-1)*(pow(N-2, K-2));
The examples are correct (also the ones I invented), but all the others, except three, are wrong.
I tried to solve it on paper. For example:
Input: 4 5
2 --> 3 --> 2 --> 3
2 --> 3 --> 2 --> 4
2 --> 3 --> 4 --> 2
2 --> 3 --> 4 --> 3
2 --> 4 --> 2 --> 3
2 --> 4 --> 2 --> 4
2 --> 4 --> 3 --> 2
2 --> 4 --> 3 --> 4
*3 (N-1)
Output = 24
I might have missed something in the problem description.
If you know what might be the problem here, please let me know.
Thanks.

2

You also have to consider that he can return to the first intersection during his walk (unless it is the penultimate intersection)
The total number of paths for N = 4 and K = 5 is 60

1 Mi Piace
3

I can’t figure out the formula. Could you help me a bit more?

4

Vorrei sapere come si ottiene 100/100 in questo programma

Ho individuato che la formula per calcolare il risultato contiene una specie di serie geometrica:
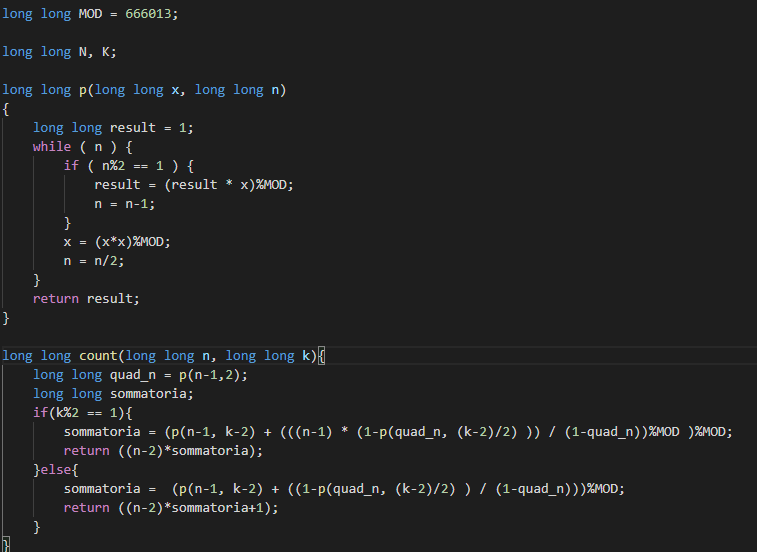
Cattura

Però questa soluzione prende solo 30/100, penso perchè nei casi con valori in input molto alti, nella formula per il valore della somma parziale della serie geometrica il numeratore andrebbe in overflow e la divisione non è corretta.

Cattura2
Questa soluzione, che calcola la somma parziale della serie con un ciclo, è corretta ma troppo lenta, fa 80/100.

Quale sarebbe la soluzione 100/100?

5

In realtà non è vero che non puoi fare le divisioni in Z_p (gli interi modulo p). Per un intero a, b è un suo inverso modulo p sse a*b=1 mod p. Per il teorema di Fermat, a^{p-1}=1 mod p, dunque a^{p-2} è inverso di a, quindi se vuoi fare una divisione per a, basta moltiplicare per a^{p-2}.

6

I don’t know if there are other solutions, but you can calculate the total number of paths (N-1)^(K-1), then subtract all the paths that end in 1 (which happens to be all the paths at K-2 that do not end in 1), to calculate that you have to think about all the paths leading to K-3 and so on until K = 1

7

Grazie funziona, ho due domande: sai se ci sono altre soluzioni a questo problema, e cosa posso vedere per capire quello che mi hai consigliato, perchè è una cosa a me totalmente ignota.

8

But how do I get all the paths at K-2 that don’t end in 1?

9

Allora, per altre soluzioni a questo problema, le prime cose che mi vengono in mente sono divide and conquer e matrix exponentiation, mentre per sapere di più su perchè a^{p-2} è inverso di a, credo sia spiegato decentemente qui e girando un po’ fra le pagine.

1 Mi Piace
10

The answer is the same as with K-1: you have to subtract all the paths that end with 1 in K-3

11

So is it something like this?

   for(int i = 2; i <= K; i++){
        sub += pow(N-1, K-i);
    }
    answer = pow(N-1, K-1)-sub;

I don’t quite understand.

12

The idea is something like (N-1)^(K-1) - (N-1)^(K-2) + (N-1)^(K-3) - (N-1)^(K-4) + … until K = 1.
With 3 4 it becomes 2^3 - 2^2 + 2 = 6 with paths:
1 --> 2 --> 1 --> 2 V
1 --> 2 --> 1 --> 3 V
1 --> 2 --> 3 --> 1 X
1 --> 2 --> 3 --> 2 V
1 --> 3 --> 1 --> 2 V
1 --> 3 --> 1 --> 3 V
1 --> 3 --> 2 --> 1 X
1 --> 3 --> 2 --> 3 V

13

Thanks a lot. I think I understand it now. The examples I tried are all correct, but the subtasks 3 - 5 are wrong (Subtask 5 -> Execution timed out).

for(int i = 1; i < K; i++){
    	if(i%2 == 0){
    		answer -= fmod(pow(N-1, K-i), MOD);
    	}else{
    		answer += fmod(pow(N-1, K-i), MOD);
    	}
}
printf("%lld\n", answer%MOD); // print the result
    return 0;
14

You have to consider that calling the power function for each value up to K is pretty inefficient, I would suggest to start from the bottom and try to avoid using the power function